Rémi Flamary

SVM et régularisation

$$ \def\w{\mathbf{w}} $$

Dans cette démo, nous allons illustrer l'effet de la régularisation et du paramètre de noyaux pour la discrimination à l'aide de Séparateurs à Vaste Marge (SVM).

Introduction rapide aux SVM

Les SVM permettent d'apprendre une fonction de discrimination à travers le problème d'optimisation suivant:

où C est un terme de régularisation qui pondère l'attache aux données (terme de gauche) et la régularisation (terme de droite). L'attache aux données consiste en une mesure d'erreur sur une liste d'échantillons d'apprentissage ${\mathbf{x}i,y_i}{i=1\dots n}$ contenant les examples $\mathbf{x}_i\in\mathbb{R}^d$ et la classe correspondante $y_i\in{1,-1}$.

Un des avantages des SVM est leur capacité à utiliser une représentation complexe des données à l'aide d'une fonction noyaux $k(\cdot,\cdot)$ qui mesure la similarité entre deux exemples. La fonction de décision est aisni de la forme

En pratique, le noyaux Gaussien (aussi appelé RBF) défini par

est régulièrement utilisé lorsuqe la fonction de décision est non-linéaire.

Lorsque l'on utilise les SVM avec un noyau gaussien, il est nécessaire de choisir 2 paramètres importants: C et $\gamma$. Dans cette démo, nous illustrons sur un exemple simple l'effet de ces deux paramètre sur la fonction de discrimination SVM.

Problème de discrimination

Dans cette démo, nous illustrons les SVM sur une problème de discrimination 2D appelé "clown". Ce problème a l'avantege d'être facile à comprendre et visualiser sur une figure 2D.

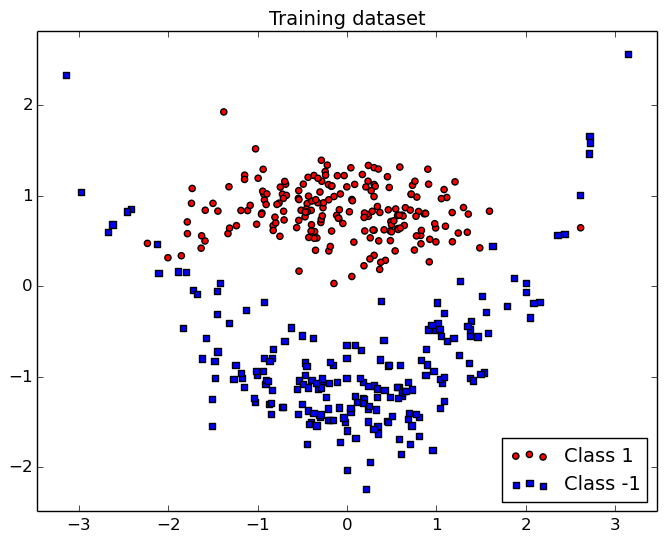
Dans cette figure, on peut voir que la fonction de discrimination entre les deux classes est non-linéaire mais de complexité limitée.

Démo de régularisation

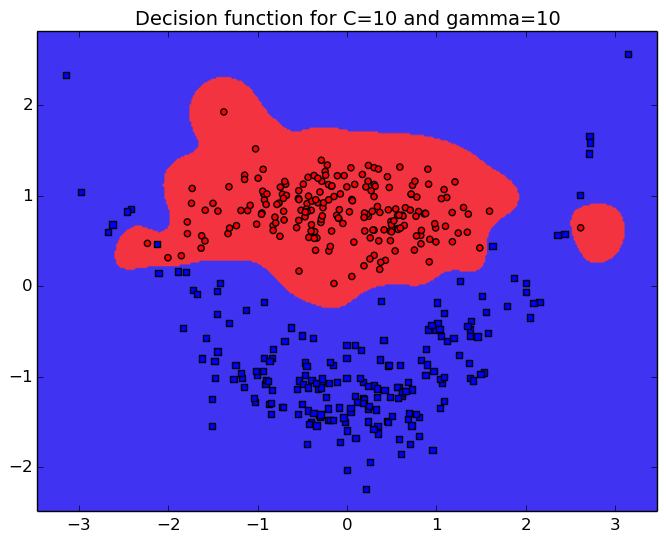
La paramètre C promeut des fonction lisses pour de petites valeurs, tout comme le paramètre $\gamma$ qui définit le voisinage des points. On reporte également le taux de bonne reconaissance du classifieur (TBR) c'est à dire sa capacité à prédire la classe de nouveux exemples.

Références

Pour plus d'informations sur les séparateurs à vaste marge je recommende [1] qui est un livre d'introduction classique. Un trés bon cours de Stéphane Canu est également disponible sur le web [2].

Les figures de cette démo ont été générées avec Python,Numpy, et Scikit Learn. Le code est disponible ici.

[1] Learning with kernels: support vector machines, regularization, optimization, and beyond, B Scholkopf, AJ Smola, 2001, MIT Press.

[2] Cours SVM, S. Canu.