Rémi Flamary

Professional website

En flag English
En flag Français
En flag Zorglangue

Pages

Other sites

Contact

todo qrcode

Address

Centre de Mathématiques Appliquées (CMAP)
École Polytechnique
Route de Saclay
91128 Palaiseau Cedex
FRANCE

SVM and regularization

\(\def\w{\mathbf{w}}\)

In this demo, we illustrate the effect of regularization and kernel parameter choice on the decision function of support vector machines (SVM).

Short introduction to SVM

The decision function of a support vector machine classifier is obtained through the minimization of the following optimization problem:

$$ \min_{f}\quad C\sum_{i=1}^{n} \max(0,1-y_i f(\mathbf{x}_i)) + \|f\|^2 $$

where C is a regularization parameter that balances the data fitting (left hand term) and the regularization (right hand term). Note that the data fitting term uses a training set $\{\mathbf{x}_i,y_i\}_{i=1\dots n}$ that consists in a list of samples $\mathbf{x}_i\in\mathbb{R}^d$ and their associated class $y_i\in\{1,-1\}$.

One of the strengh of SVM is their ability to chose a complex representation of the data thanks to the use of a kernel function $k(\cdot,\cdot)$ that measures the similarity between samples. The decision function is of the form

$$ f(\mathbf{x}) =\sum_{i=1}^n \alpha_i y_i k(\mathbf{x},\mathbf{x}_i) $$

In practice the Gaussian kernel (also known as RBF) defined as

$$ k(\mathbf{x},\mathbf{x}')=\exp{(-\gamma \|\mathbf{x}- \mathbf{x}'\|^2)} $$

is often used when the decision function has to handle non-linearities.

When using SVM with a gaussian kernel, one has to select two important parameters: C and $\gamma$. In this demo we illustrate the effect of those parameters on the final decision function of the SVM.

Dataset used in the demo

In this demo, we illustrate SVM using a 2D non-linear toy dataset also known as "Clown". The main advantage of a 2D example is that it is easy to plot and visualize the samples of each classes in a classical scatter plot figure as shown below.

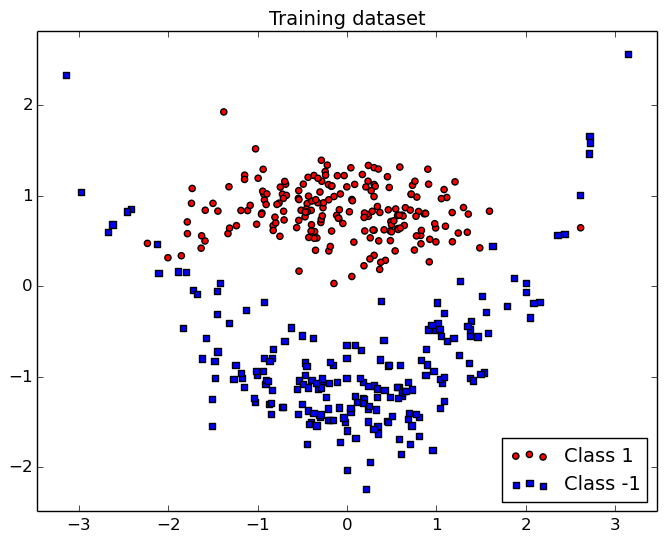
training samples

In this Figure, we can see that a non-linear function has to be used for a correct classification but the complexity of the fonction is limited. As illustrated in the next section, the parameters have to be chosen carefully.

Regularization demo

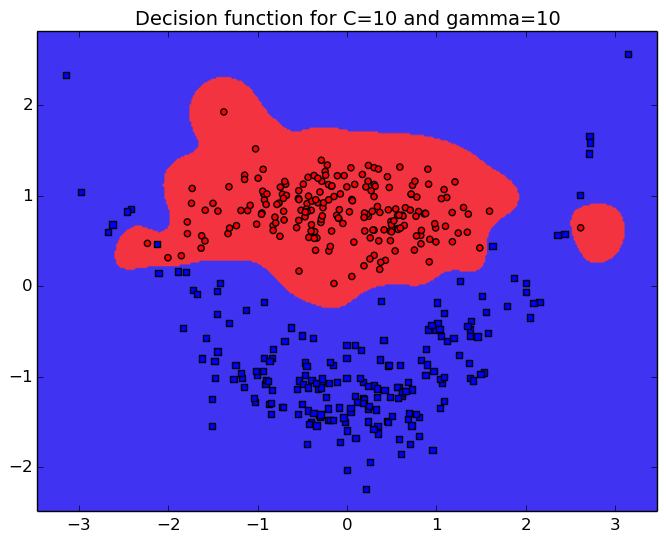
classification result

Regularization parameter C

Kernel parameter gamma

Performance
Rec. rate

Current value: C=10

Current value: gamma=10

RR=0.9754

The C parameter that will balance the data and regularization term, which will promote smooth decision function when C is small. The parameter $\gamma$ of the gaussian kernel is also extremely important as it will define the neighborhood of the samples. A large $\gamma$ leads to more complex function. The precision of the classifier on a large test sample is also reported on the right as RR (for recognition rate).

References

For more information about Support Vector Machine, I strongly recommend [1] that is a classic introduction. A very good course by Stéphane Canu is also available online [2].

The figures have been generated using Python,Numpy, and Scikit Learn. The code is avalable here.

[1] Learning with kernels: support vector machines, regularization, optimization, and beyond, B Scholkopf, AJ Smola, 2001, MIT Press.

[2] Understanding SVM, S. Canu.